Breaking Down Ranked Choice Voting

Written by Michael Leon on 19 November 2024

Updated on November 19, 2024

With the election results fresh on everyone’s minds, Americans are once again dissatisfied with the two party system and wish for something better. The Pew Research Center reported back in 2022 that tensions are growing amongst the two parties, and the American political landscape is as divided as ever. This rings true with the results of the 2024 presidential race coming in and the two parties as split as they’ve ever been. According to that same study, almost 40% of those surveyed say that they very much or extremely agree with the desire for more political parties to choose from.

Several states and municipalities have adopted a ranked choice voting system (RCV), with the District of Columbia being the most recent to do so, garnering 73% support from voters across the District as of November 5th. Many support the idea as a way of beginning to bring third-party candidates into the fold. Today we’re going to be taking a deep dive into ranked choice voting systems, how they work, and some of the math going on behind the scenes in an election.

Constructing a Ranked Choice Voting System

As you can probably guess, an RCV system has voters rank candidates on their ballot based on preference. If there were, say, 5 candidates, then one voter’s ballot may look like Candidate 2, Candidate 1, Candidate 4, Candidate 5, Candidate 3.

We’ll look at how Virginia conducts their ranked choice voting (which, right now, is exclusive to Arlington County): It starts by counting all first choice votes. If nobody reaches a majority, then the candidate with the fewest votes is eliminated, and anyone whose ballot had that candidate as their first choice has their second choice vote counted. This continues down the ballot until a candidate reaches a majority.

The issue, here, is that this reduces to a majority rule system anyways. So how can we do better? Is there a “best” system out there? Here, we look to the work of Kenneth Arrow for an answer. His work sought to answer that, given a set of reasonable axioms, or rules, about voting, can you construct a fair ranked choice system?

Let’s lay out those axioms:

1. Each voter ranks every candidate, and if a candidate is ranked at a certain position, then every candidate ranked below them is less preferable. We call this completeness.

2. If Candidate A is preferred to B, and B is preferred to C, then A is preferred to C. We call this transitivity.

3. This is a non-dictatorship. In this sense, dictator means one voter is controlling the outcome of the election, so this axiom is stating that the results do not only depend on only one person.

4. It is possible for any candidate to beat any other candidate, given some combination of votes, i.e. that voters are not ignored in the results. To extend this, if every voter prefers candidate A to candidate B, then A should beat B. This extension is known as Pareto efficiency.

5. If every voter prefers A to B, and the preference of B and C changes, the relative ranking of A and B should not. This is to say that relative rankings are pairwise independent.

Sounds reasonable, right? Well, Arrow shows us that playing under these rules, we have a very hard time setting up a fair voting system. In fact, he shows us that it’s impossible.

Arrow's Impossibility Theorem

To put it simply, Arrow’s theorem states that if an election has at least three candidates, then it is impossible to have Pareto efficiency, non-dictatorship, and independence of irrelevant alternatives satisfied. Because the US uses a majority-rule system in its RCV system, most of these issues are actually circumvented by design. But let's look at a textbook example. Suppose we have 3 candidates, A, B, and C, and 3 voters, 1, 2, and 3. If voter 1 ranks A > B > C, voter 2 ranks B > C > A, and voter 3 ranks C > A > B, what do we do? It's impossible to claim any of the candidates won, as the same logic would apply to each of the others. Practically speaking, this would be a tie, and would require a recount or another election to be held.

There is a case in which Arrow's theorem does not hold, though, and this is if we arrange our voters and candidates on a Left-Right spectrum.

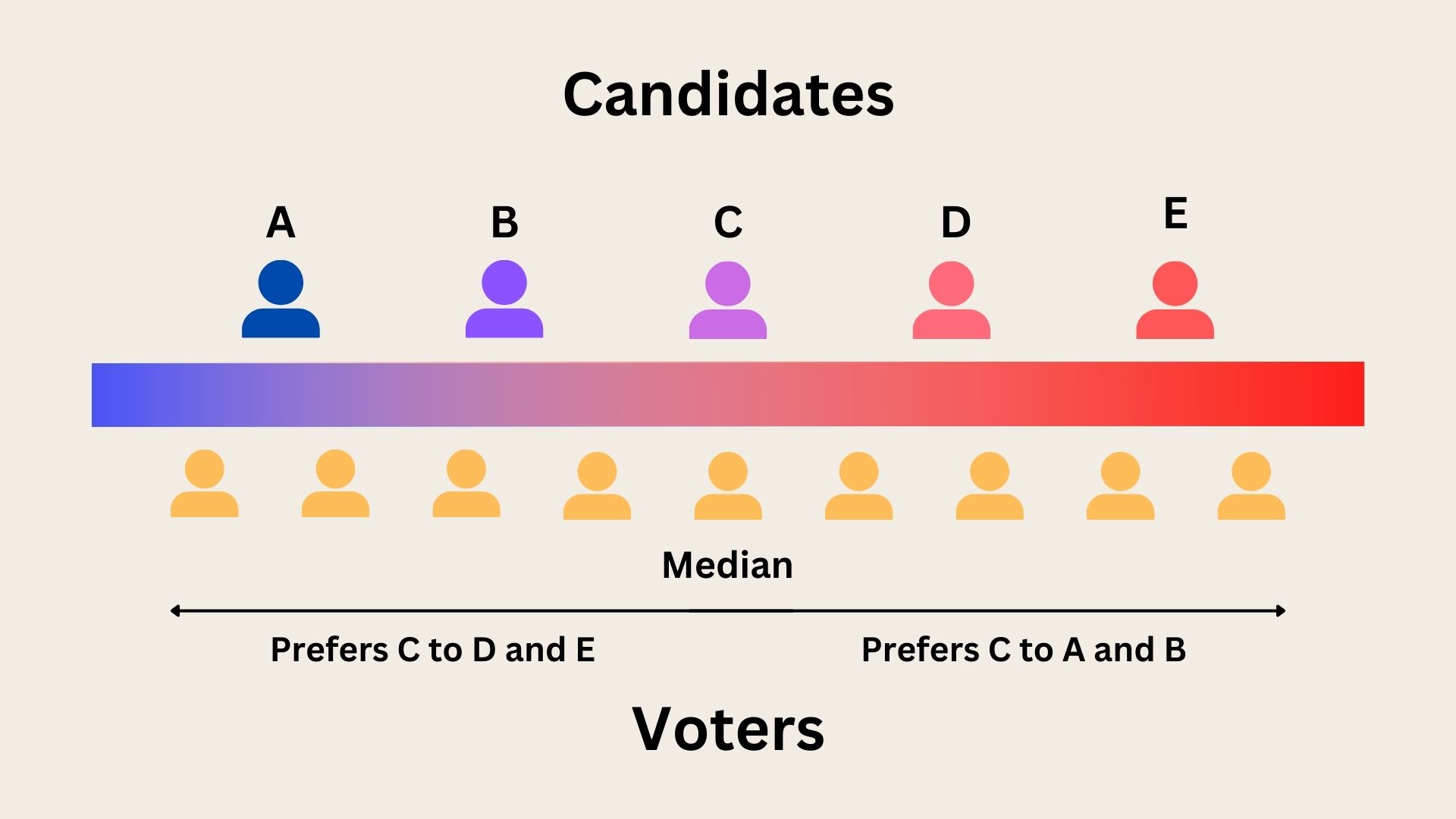
Median Voter Theorem

Suppose that we arrange our voters and candidates on a spectrum from left to right, as we might expect to see with the political spectrum. We also suppose that each voter’s support for a candidate has a maximum somewhere on this spectrum, and as the candidate moves away from that spot in either direction then their support decreases. 

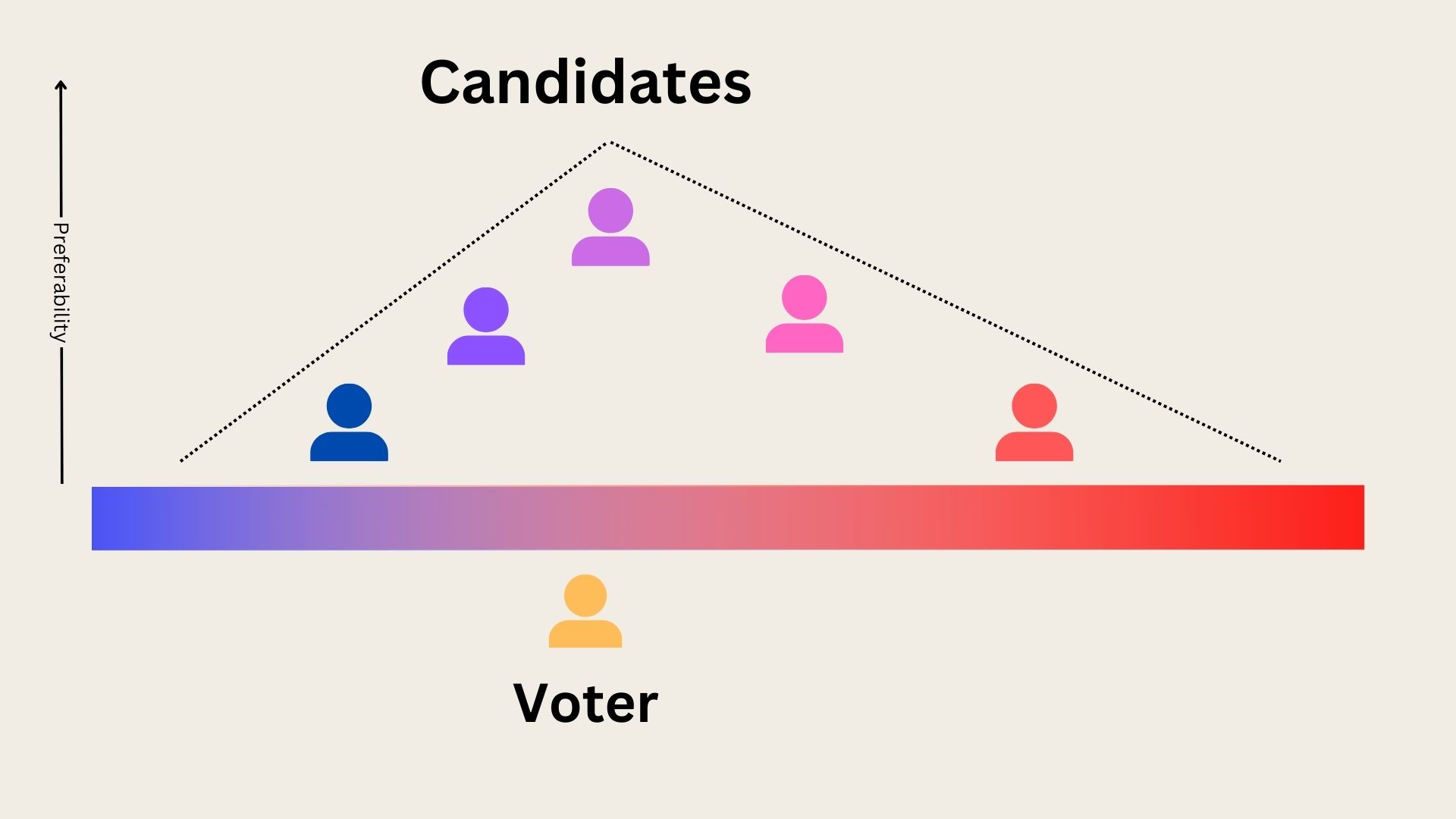
The median voter theorem simply says that candidates, under this system, are going to gravitate towards the median voter.

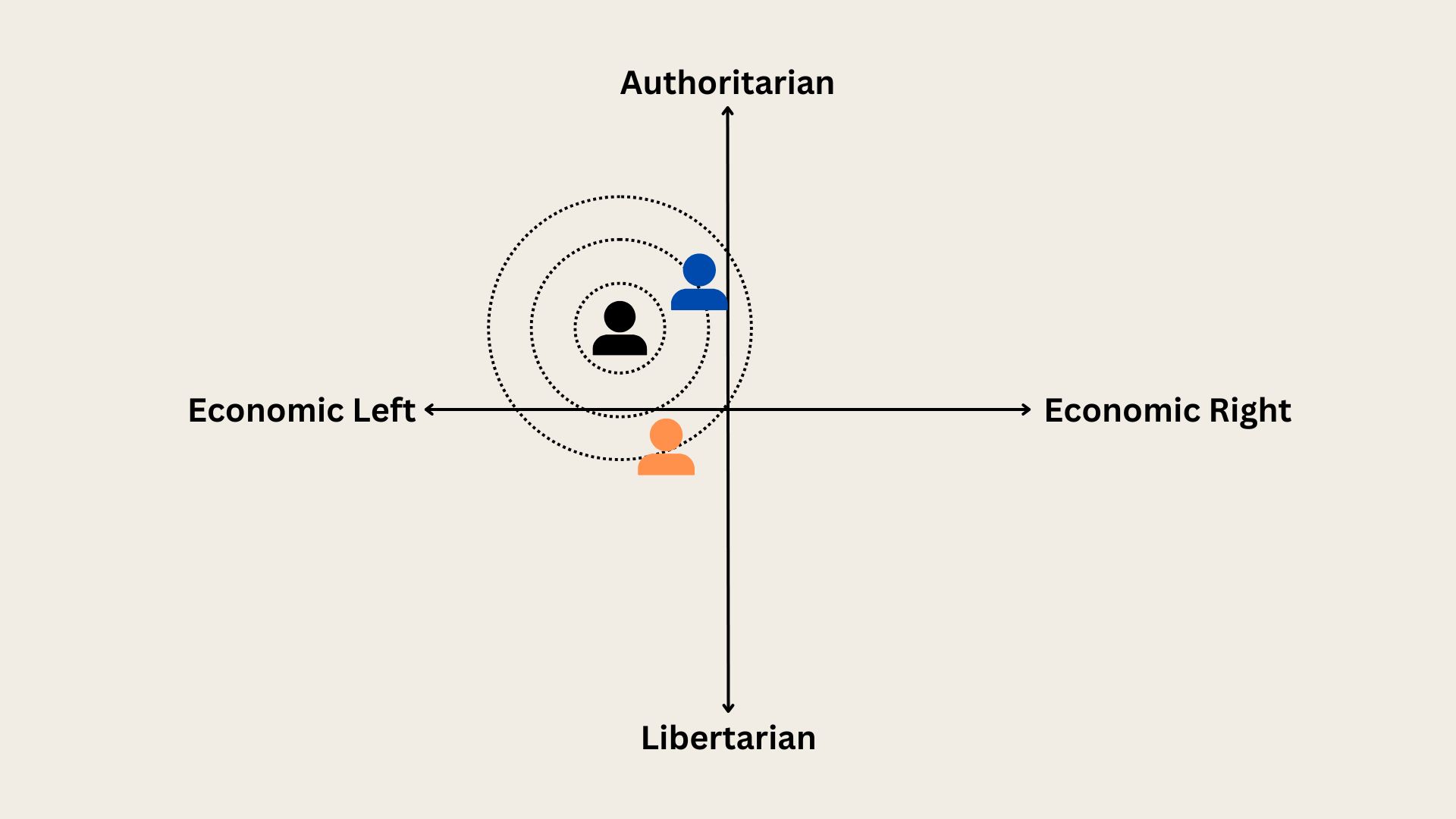
Now, this idea falls apart when we break away from just one dimension. If we view candidates on, say, a political compass, then it becomes impossible to gravitate towards any median, because the median simply does not exist. A voter has a preferred placement on the compass, in the diagram below that would be the candidate at the center of the circles, and as candidates move away from this in any direction they get less preferable. The dashed circles represent indifference curves, meaning that if two candidates both fall on a curve then they are equally preferable.

When we introduce more voters, though, things get tricky. Where should a candidate position themselves to be most preferable?

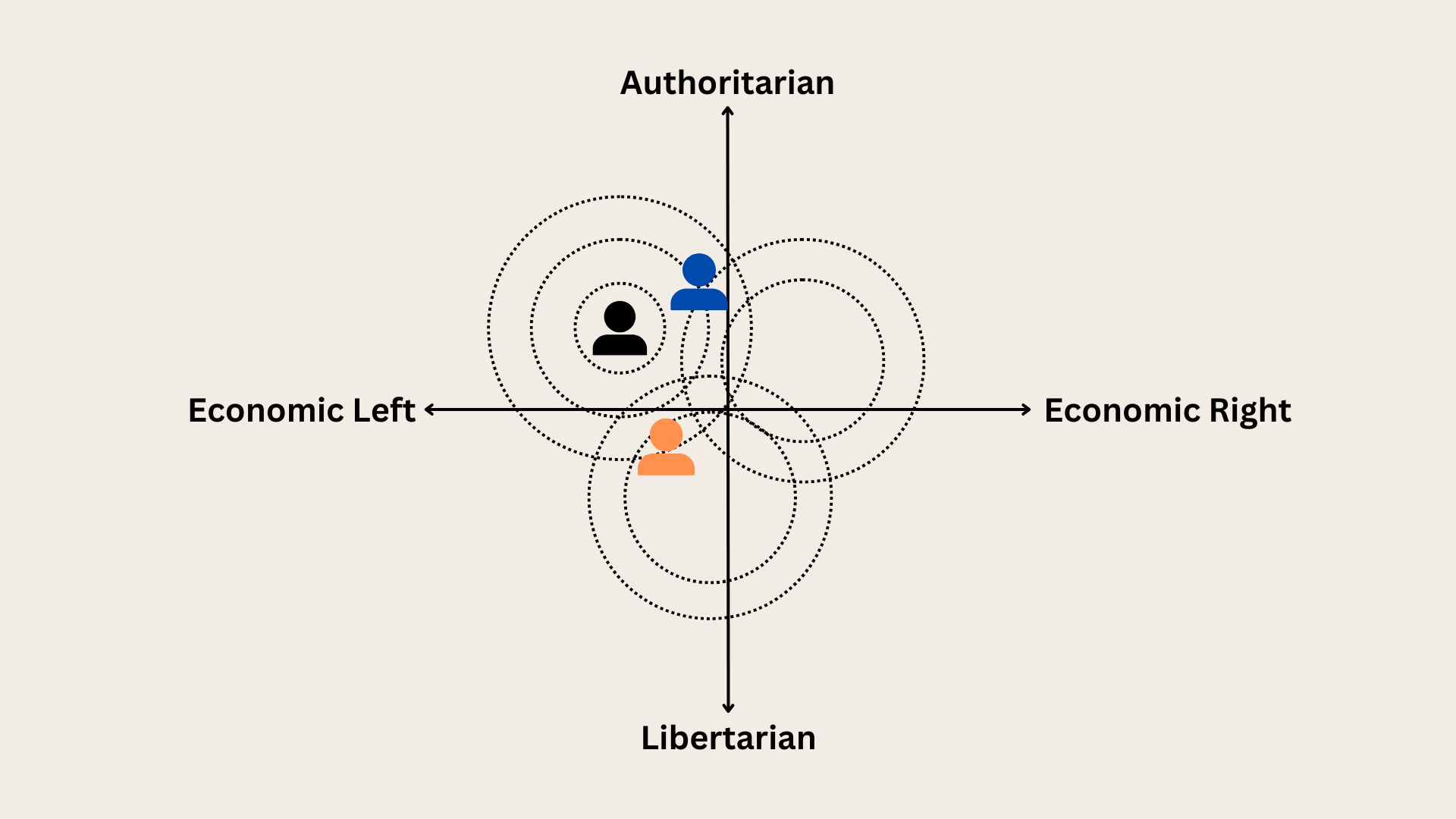
In this case, you might think that the solution is to place yourself at the center of all 3 indifference curves. However, if another candidate placed themselves so that they were slightly more preferable for two voters, then they would win overall. In this instance, there is no “most preferable position,” meaning that if we used a strict ranking system as Arrow suggests, we once again have an impossible outcome.

From a voter's perspective

One argument against ranked choice voting is that it’s too confusing, that it puts more of an onus on the voter. Admittedly, yes, it does require the voter to know the candidates and how they rank them. But, in some sense, it’s fairly intuitive. How does a voter approach the ballot, though, and how should candidates campaign?

For this, we're going to assume a reasonably informed voter, who knows both what issues they’re voting on and what the candidates’ responses to those issues are.

Suppose each voter has a number of issues \(i_1, \dots, i_k\)that are important to them for the upcoming election. Suppose that there are \(a_1, \dots, a_k\) weights associated with this such that \(\sum_{m=1}^k a_m = 1\). For each issue, a candidate is either favorable or not. If they are favorable, then they get assigned a 1 on this issue, if they are not then they are assigned a 0.

Now this is, obviously, a naive approach. It makes a lot of assumptions, and says that there cannot be any partial preference for one candidate on an issue, operating as a winner-take-all on an issue-by-issue basis, and only ranking at the end.

So, let’s do better. Let's say we have \(n\) candidates. For each issue, let’s have a preferability vector \([ c_1 \cdots c_n]\), where the overall preferability adds up to 1. Then we can say that overall preferability is \([p_1 \cdots p_n] = \displaystyle\sum_{m=1}^k a_m [c_1 \cdots c_n]_m\), and that a voter will decide their rankings solely based on this preferability.

As a candidate, you’ll have some vague estimates for the weighting of issues across all demographics, and more granular survey data can give you approximate weights within a demographic. The goal of each candidate, then, should be to maximize their average preferability.

It's through this lens that we can view the tendency of politicians to adopt more centrist positions. We can view each individual issue as being single-peaked for each voter, meaning that each voter has a stance on a policy they deem most preferable, and as a candidate moves away from this in either direction, their preferability declines. So for each issue, the Median Voter Theorem applies, meaning that as a whole it should apply too. The winning strategy will be to be as close to the median as possible without alienating voters. 

Through this lens, too, we can get a glimpse at what went wrong for Kamala Harris in the 2024 election. She, like most politicians, adopted a centrist stance on a lot of issues. This time around, though, it didn't work. Why? At the risk of oversimplifying things, she overestimated what voters would be willing to put up with. On the left hand of the spectrum, we saw people not vote, rather than voting for someone they deemed as too far removed from them. At the time of writing, Kamala Harris sits just shy of 74 million votes, a far cry from Joe Biden's 81.2 million in 2020. 

Elections don’t play out based solely on math and policy, they play out based on emotion and sentiment, too. Increasingly, Americans are turning away from mainstream news and distrusting it more and more, with only 59% of adults saying they trust information from national news organizations, down from 76% in 2016.  The difference is even more stark if you look at just Republicans, who have seen a drop from 70% to 40% in the same time frame, according to the Pew Research Center. Voters are getting a larger share of their information from social media and directly from the candidates. In short, politics is politics; it’s important to be popular and to say the right things, and this is true perhaps now more than ever. The key is in the messaging.

The desire for more political parties, more choice, is strong. Americans are growing tired of divisive messaging, of pitting neighbor against neighbor. Ranked choice voting serves as a way to develop third party support, to allow everyone to feel as though their voice has been heard. It aims to reconcile the feelings of voters who tend to sit out elections when their supported candidate isn't running. If you'd like to learn more, or figure out how you can get involved, check out fairvote.org

Links to all sources:

[1] Pew Research article on the tensions between the two parties.

[2] District of Columbia adds Ranked Choice Voting.

[3], [4] Resources for Arrow's Impossibility Theorem.

[5] Resource for the Median Voter Theorem.

[6] Pew Research article on American Adults' trust of news outlets.

[7] Fairvote.org